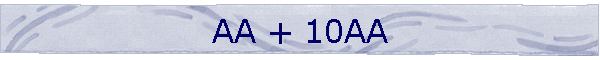
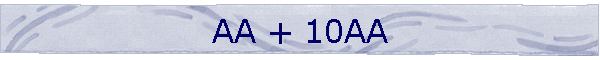
[ Home ] [ FOIL Method ] [ Double & Half Method ] [ Squaring Numbers ] [ Squaring Num End In 5 ] [ Squaring Num End In 6 ] [ Squaring Num End In 7 ] [ Squaring Num End In 8 ] [ Squaring Num End in 9 ] [ Squaring Nums 40-49 ] [ Squaring Nums 50-59 ] [ Squaring Nums 90-99 ] [ Difference of 2 Squares ] [ Mult Nums End in 5 ] [ Mult Nums One's Add 10 ] [ Mult Nums One's Add 5 ] [ Mult Nums Same Ten's Digits ] [ Mult Nums Tens Add 10 ] [ Mult Nums Less 100 ] [ Mult Nums More 100 ] [ Mult Nums More 100 Less 100 ] [ AB + BC ] [ AA + 2AA ] [ AA + 3AA ] [ AA + 7AA ] [ AA + 10AA ] [ Mult Nums Less 1000 ] [ Mult Nums More 1000 ] [ Add 2 Squares ] [ Product of 4 Nums ] [ Adding Consecutive Squares ] [ Squaring: 101a ] [ Adding Squares #2 ]
(*View/Download
.pdf file)
(**) Adding Squared Numbers In The
Form: a2 + (10a)2:
A.
This method is very easy since from algebra we know:
a2 +
(10a)2 = 101a2
B.
Therefore, you square the smaller number, then multiply
by 101 for the answer.
Ex [1] 142 + 1402 =_________.
a)
142 = 196.
b)
196 x 101 = 19796.
c)
The answer is 19796.
Ex [2] 312 + 3102 =_________.
a)
312 = 961. See Squaring
Numbers.
b)
961 x 101 = 97061.
c)
The answer is 97061.
Back to top