|
||
| HOME
Miscellaneous Elementary Junior High Sum Of Positive Integral Divisors High School Manipulating Polygonal Numbers
|
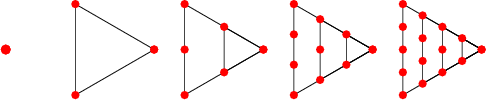
Triangular Numbers:
A. Triangular numbers are numbers that create triangles. In other words 1, 3, 6, 10, 15, 21, etc. B. Triangular numbers can be calculated by 1, 1+2, 1+2+3, 1+2+3+4, etc. C. See Adding Sequences. D. The nth triangular number can be calculated by the equation: 1 + 2 + ... + n = n (n+1) 2 E. There are various ways of using triangular numbers: 1. Calculating the nth triangular number. a. Use the formula: n(n+1)/2. 2. Finding the triangular number from a given number. a. Solve the formula: n(n+1)/2 = x, where x is the number. 3. Adding successive triangular numbers. a. Use the formula: n2, where n is the larger of the two triangular numbers. NOTE: This is because 2 triangles back to back make a square. 4. Subtracting 2 successive triangular numbers. a. The answer is simply: n, where n is the larger of the two triangular numbers. F. Below are a few examples: Ex [1] Find the 10th triangular number. a. Using the formula we get: (10)(11)/2. b. This reduces to (5)(11) or 55. c. The answer is 55. Ex [2] The 8th plus the 9th triangular number is __________. a. Since 9 is the largest, we use: 92 or 81. b. The answer is 81. Ex [3] The 11th minus the 12th triangular number is _______. a. We just use the largest number, which is 12. b. However, the answer is going to be negative since the 12th triangular number is larger than the 11th. c. The answer is -12.
|