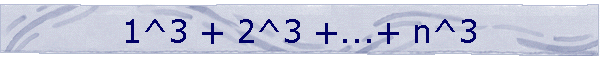
A. A sequence in this form reduces to:

B. Notice that this expression is the same thing as: (1 + 2 +...+ n)2
1. Multiply the last number by that number plus 1, then divide by 2.
2. Square this result.
Ex [1] 13 + 23 +...+ 103 =_________.
a) Using the expression this reduces to: (10)(11) / 2 = 5 x 11 = 55.
b) 552 = 3025. See Squaring A Number Ending In 5.
c) The answer is 3025.
Ex [2] 13 + 23 +...+ 153 =_________.
a) Using the expression this reduces to: (15)(16) / 2 = 15 x 8 = 120.
b) 1202 = 14400.
c) The answer is 14400.