

A. There are many different ways of working with vectors and vector spaces. The following ways are only possibilities for a number sense test. It is possible they will never show up.
B. Dot Product
1. The dot product of a vector, x . y, is defined as being:
![]()
where x = (x1,x2,...,xn) and y = (y1,y2,...,yn)
Ex [1] The dot product of the vectors (3,4) and (-1,5) is ______
a. The answer is 3(-1) + 4(5) = 17.
Ex [2] The dot product of the vectors (0,1,1) and (5,4,-3) is _____
a. The answer is 0(5) + 1(4) + 1(-3) = 1.
C. Cross Product
1. To find the cross product of 2 vectors, you need to be familiar with determinants of matrices.
2. The cross product of 2 vectors (of dimension 2), u x v, is defined as:
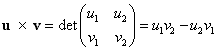
Ex [1] The cross product of the vectors (3,5) and (-1,3) is _____
a. The answer is 3(3) - 5(-1) = 14.
Ex [2] The cross product of the vectors (-1,a) and (-2,4) is 6, so a = ______
a. This problem is a little more complicated. Just set up an algebraic expression.
b. -1(4) - (-2)a = 6 or -4 + 2a = 6. Solving for a we get a = 5.
c. The answer is 5.
D. Norm
1. The norm of a vector, ||u||, is defined as being:
![]()
2. Knowing Pythagorean Triples will be helpful.
Ex [1] Find the norm of the vector (0,12,5) _____
a. You should know the Pythagorean triple (5,12,13). The answer is 13.
b. If you
don't know this, you can see that ![]() .
.