
A. Number Sense only deals with small matrices, usually 2 x 2 matrices. This page will look at 3 ways of manipulating matrices: Multiplying Matrices, Inverses, and Determinants.
B. Multiplying Matrices
1. Unlike general multiplication, matrix multiplication is not commutative. Multiplying A x B and B x A will give different results.
2. The following will show how to multiply two 2x2 matrices:
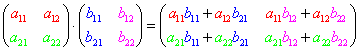
a. In other words, you multiply the row of the matrix on the left with the column of the matrix on the right.
Ex
[1] ![]() ,
then d = _____?
,
then d = _____?
a. Since we are looking for d, then we are only concerned with that spot. So d = 3(2) + 0(5) = 6. The answer is 6.
b. Some people have a hard time knowing which row and column to multiply. This is how I usually think of it. If I were to put the two matrices on top of each other, which row from the first matrix and which column from the second matrix would they intersect on. In this example, it is the second row of the first matrix, and the second column of the second matrix.
3. This method of multiplication can be expanded to matrices other that 2x2. However, due to space constraints, on a test, usually you will only see a 2x2 matrix or smaller.
C. Inverses
1. In general, inverses are very difficult to compute. However, on 2x2 matrices, inverses are easy.
2. For a 2x2 matrix:
![]()
Ex
[1] 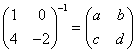 ,
then c = ____.
,
then c = ____.
a. According to above, c = -4. The answer is -4.
D. Determinants
a. In linear algebra, determinants have many uses. Like with inverses, finding the determinants can prove difficult. However, on a 2x2 matrix, determinants are easy.
b. Determinants are usually abbreviated "det". So:
![]()
Ex
[1] ![]()
a. The answer is 3(5)-(2)(-1) = 15+2 = 17.