

A. To find the maximum and minimum values of a polynomial, you need to understand derivatives.
B. A maximum value of a polynomial is when the graph changes from increasing to decreasing.
C. A minimum value of a polynomial is when the graph changes from decreasing to increasing.
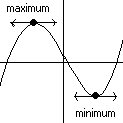
D. If you look at the slope of the lines at the maximum and minimum points, you will notice that the slope is 0 at those points. Since derivatives tell you the slope, if we take the derivative and set it equal to 0, we will find out at which values of x are the maximum or minimum points.
E. The second derivative will actually tell us if the point is a maximum or minimum point. Whatever x-values are found from the first derivative can be plugged into the second derivative. If it is positive, it is a minimum point. If it is negative, it is a maximum point.
F. Examples
Ex [1] The maximum or minimum points of the equation y = ax2 + bx + c is _______.
a. Taking the derivative and setting it equal to 0, we get: 2ax + b = 0.
b. Solving for x gives: x = -b/2a.
c. The second derivative is 2a. So if a is positive, then x= -b/2a is a minimum. If a is negative, x= -b/2a is a maximum.
d. This example was set here to show you where the equations came from for the vertex of parabolas. Sometimes, knowing why a formula works will help you to remember it.
Ex [2] The maximum point of the graph y = x3 + 3x2 - 9x + 2 is (a,b). Then a = _______.
a. First take the 1st derivative which is 3x2 + 6x - 9 = 0 or 3(x2 + 2x - 3) = 0.
b. We can factor x2 + 2x - 3 to (x-1)(x+3) = 0. So x = 1 or x = -3.
c. One of these values is a minimum and one is a maximum. To find out which is which we can use the 2nd derivative or 6x + 6. If we use x=1, we get a positive number so x=1 is a minimum. If we use x=-3 we get a negative number, so x=-3 is a maximum.
d. The answer is a = -3. If the question had asked for the 'b' value, then you would need to plug in -3 to the original equation or (-3)3 + 3(-3)2 - 9(-3) + 2 = -27 + 27 + 27 + 2 = 29.
G. On number sense tests, the maximum/minimum value problems will most likely be polynomials of degree 2 or a quadratic equation. If this is the case, I suggest using the rules for the vertex of parabolas to find the maximum/minimum values. In other words, if (a,b) is the maximum/minimum point use the formulas for (h,k) in parabolas.