A. An integral is basically the exact opposite of a derivative.
B. An
integral gives the area under a curve from the x-axis to the curve from a
specified range. An integral is expressed by the symbol: 
.
C. Below are some basic rules for computing integrals:
1. The integral of a constant, c, is cx.
2. The
integral of xn is 
.
3. The integral of a*f(x), where a is a constant, is equal to a times the integral of f(x). (*Basically, you can factor out the constant*)
4. The
integral of f(x) 
g(x) = 
.
a. In this problem, we can take each term separate.
b. The integral of 3x2 = x3; of 2x = x2; of 1 = x.
c. The answer is x3+x2+x+C
d. We usually add a C on the end because the integral of 0 is a constant.
D. You should notice, that if you take the derivative of the new function, you will end up with the original function.
E. Common Integrals:
1. The integral of sin(ax) = -1/a cos(ax)
2. The integral of cos(ax) = 1/a sin(ax)
3. The integral of sec2 x = tan (x)
4. The integral of e(ax) = 1/a e(ax).
5. The integral of 1/ax = 1/a ln(ax)
F. These are just some of the common integrals. There are lots of integrals in many different forms, which can be found on the front or back cover of most calculus books.
G. When calculating an integral in a specified range:
a. To compute this integral take each term separate and get: x3/3 - x2.
b. To find the value from 0 to 3, first plug in 3. Doing so gives: 33/3 - 32 = 9 - 9 = 0.
c. Next find the value for 0. This gives: 03/3 - 02 = 0.
d. The answer is 0 - 0 = 0.
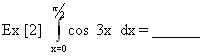
a. The integral of cos 4x is sin 4x/4.
b. To find
the value from 0 to 
we
must first use .
Doing so gives: sin 3(
/2)/3
= sin(3/2)/3 = -1/3.
c. Next, find the value for 0. This is sin 0/4 = 0.
d. The answer is -1/3 - 0 = -1/3.
a. The integral of x2 - 2 is x3/3 - 2x.
b. Plug in 4 and get 64/3 - 8 = 40/3.
c. Plug in 1 and get 1/3 - 2 = -5/3.
d. The answer is 40/3 - (-5/3) = 45/3 = 15.